今回の記事はCCNA/CCNPの方がメインの読者と想定しますが、CCIE勉強中の方も見ている想定で書いています。
CCNA勉強中の方は、「EIGRPを含むIGPって何でこんなに複雑なんだろう!」って思っている人も多いはず。
この思いは、勉強をすればする程、逆転します。
つまり、「何て本質的にはシンプルにできているんだろう!」と思うようになります。
この記事は、EIGRPのSuccessor/Feasible Successor選定について、本質的なところに出来るだけ焦点を当てました。この記事を理解することで今まで以上にEIGRPが身近になるのでは?と思います。
逆に、EIGRPを全く知らない人にはちんぷんかんぷんだと思うので、まずは基礎を学んでください。
では、本題に入ります。
EIGRPのSuccessor/Feasible Successorの選定方法、理解していますか?
なんで、あのロジックでループ回避できているか、わかりますか?
その辺の基本的な疑問などもこの記事で解決しようと思います。
そもそも、Successor/Feasible Successorとは?
この記事を読んでいるという事は、これはざっくり理解していますよね。
- Successor-ルーティングテーブルに乗せるプライマリールート
- Feasible Successor-Successorが使えなくなったときに使うバックアップルート
Unequal Load Balancing等でFeasiblie Successorも同時に使うことがありますが、その辺の話は今回は省きます。
Successor/Feasible Successorの決定基準について
EIGRPでは、他のIGPと同様に、本質的にはプレフィックスまでの「コスト」の関係が決定基準です。
K値が・・・とかFormulaが・・・とかは、結局は「コスト」を算出する材料にすぎません。
この「コスト」を計算し、Successor/Feasible Successorを決定するのです。
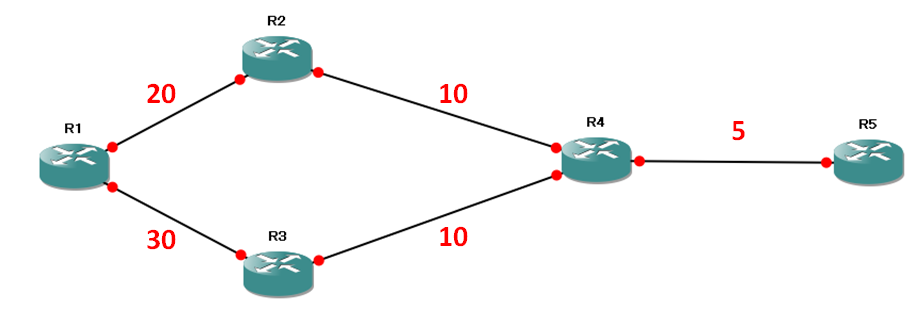
細かい解説をする為に、以下の図を例としてあげます。
赤文字が、そのリンクの「コスト」です。
R1が「R4-R5」のプレフィックスに到達したい場合の、該当プレフィックスのルートを決定するとします。
R1には2つのルートがあります。
- R1-R2のルート
- R1-R3のルート
この2ルートのどれが「Successor」・「Feasible Successor」・「いずれでもない」になるでしょうか。
Feasible DistanceとReported Distance
SuccessorとFeasible Successorの決定ロジックを理解するためには、Feasible Distance(FD)とReported Distance(RD)の理解が不可欠です。(RDはADと言われていましたが、Administrative Distanceと混同されがちなので最近はRDと呼ぶようになりました。CCIEの教科書にもそう書いています)
この2つの要素の理解が、CCNAの勉強での一つの壁だと最初は思うかもしれませんが、理解すると簡単です。安心してください。
- Reported Distance:近隣ルータが広報してきた(近隣ルータから)目的プレフィックスまでの合計コスト。
- Feasible Distance:Reported Distanceに近隣ルータまでのコストを足したもの。つまり、自分から目的プレフィックスまでの合計コスト。
先ほどの例の場合は
- R1-R2のルート:RD-15・FD-35
- R1-R3のルート:RD-15・FD-45
となります。
Successorの選定ルール
ここまで理解していると、簡単です。SuccessorはFDが一番小さいルートです。
- R1-R2のルート:FD-35
- R1-R3のルート:FD-45
R1-R2が最もコストが小さいので、Successorになります。
つまり、R1がR4-R5のリンクに通信する際、通常はR1-R2のルートを使用します。
Feasible Successorの選定ルール
ちょっとややこしい。Feasible Successorは「現在のSuccessorのFDよりも、比較対象のルートのRDが小さい」条件に当てはまったルートです。
上記の例だと、R1-R2がSuccessorです。
- Successor(R1-R2)のFD:35
- R1-R3のルートのRD:15
よって、R1-R3のルートはFeasible Successorになれます。
ややこしく感じるかもしれませんが、この記事の解説を理解したらシンプルに感じるようになるはずです。
なんで、Feasible Successorの選定ってこんなルールなの?
この問いは、EIGRPでバックアップルート(Feasible Successor)を持てるのは何故か?という本質的なポイントです。
解答は「Feasible Successorをルートとして使っても、ループを起こさない為」です。
なんで、このルールがループを起こさないと言い切れるの?
これ、超重要です。超重要ですけど、難しく考える必要はありません。むしろ、頭をからっぽにした方がわかりやすいです。
まず、この回答をする前に、一度EIGRPの性質を振り返ってみましょう。
EIGRPはDistance Vectorです。
隣接ルーターから「XXへ到達するためのコストはYY」という情報だけしか受け取りません。
例えば、前の例を再度見てみます。
R1の立場に立ってみた場合、R1はこのトポロジのどこまでが実際に見えているのでしょうか?考えたことはありますか?
答えは、以下です。
R1は上と下のインターフェースの先にR2とR3がいる事しか知りません(Helloパケットで)。
R1は上のインターフェース・下のインターフェース(R2/R3)からそれぞれルート情報を受け取っているにすぎなくて、全体のトポロジは一切知らないわけです。
この状況下で、R4-R5のプレフィックスに到達する為のルートを決定する必要があるのです。
与えられた情報は、「隣接ルーターから届いたR4-R5プレフィックスのルートのRD」と「隣接ルータ間のコスト(結果的にFD)のみ。
この状況下で、最適経路のみならず、ループフリーのバックアップ経路を算出することは、R1としては大変なんです。
感覚的にも「最適経路よりも、ループフリーのバックアップ経路を算出するのが難しそう・・・」と感じるのではないでしょうか。次に、その辺を詳しく説明します。
R1がループフリーパスを算出するためにできること・・・それは
上記の図を見れば分かる通り、R1が出来ることは限られています。
上記の黒い個所を調査する事は、R1にはできません。
R1に唯一出来ること。。。それは、「自分自身を経由している可能性のあるルートを排除すること」です。
いきなり話が飛んだと感じると思うので、以下でじっくり説明します。
自分自身を経由している可能性のあるルートとは?
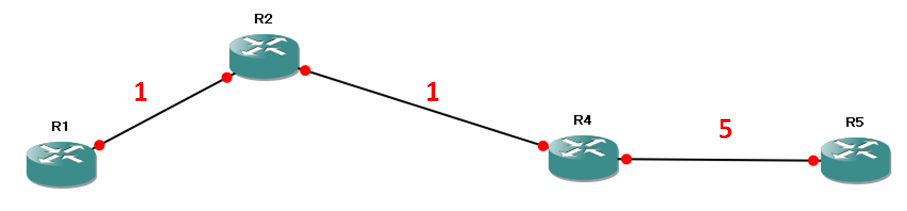
上記のトポロジをさらにシンプルにしてみます
このトポロジでR2の視点でR4-R5のルートについて考察してみましょう。
- R2はR4からR4-R5のルート(プレフィックス)を受け取ります。FDは6です。
- R2はそのルートをR1に送信します(厳密にはR2はR1を物理的には見えませんが、とりあえず左のインターフェースにR1がいるらしいという事は知っているので)
- (これはR2には見えません)R1がR2からもらったルートをR2に返したと仮定します。
(通常は返しませんが、Split HorizonをOFFにする等で返る場合もありますよね) - R2はR1からルートを受け取ります。
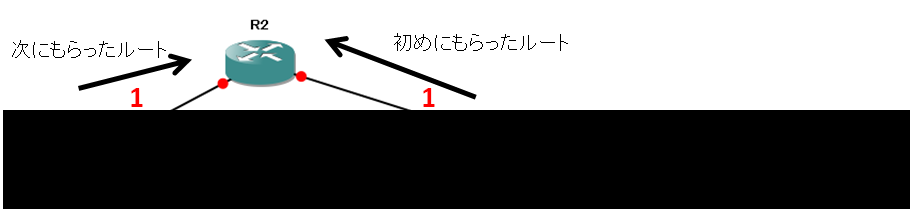
これで、R2はR4-R5に到達するためのルートを2つ持っていることになります。R2の視点からするとこんなイメージです。
R2はこの黒い個所がどうなっているかなんて分かりません。左はループしてるんですけど、そんな事わかりません。この絵だけ見たら、左に行こうが右に行こうが変わらないですよね。
まず、「絶対に、自分自身が投げたルートではない(つまり、跳ね返ってきたものではない)と言い切れるルート」があります。
それは、FDが最も小さい最適ルートです。EIGRPのルールとして、Successorを他のルータに広報するので、広報元のルートが自分を経由していることはあり得ないのです。
右からもらったルートが一番FDが小さい事は、受け取ったRDにFDを足して知っているので、右が最適という事はわかりました。
左からもらったルートはどうでしょう。最適ではないことは知っています。右(FD6)に対し、左はFD8ですから。
でも、FD8だからといって、ループしているかの証拠にはなりません。
残念ながら、R2から見て左の経路がループしているかを100%把握する術はないのです。つまり、最適ルート以外が「絶対に」ループしていないと保証することはDistance Vectorの性質上不可能です。
でも、一つ、有益な情報を算出することができます。
それは「自分自身が投げたルートを返してきている可能性があるか?」です。可能性があるか?です。絶対ではないです。
仮に自分自身が投げたルートを返してきている可能性がある場合、そのルートは自分の持っている最適ルートのFDよりもRDが大きいはずです。
上記のトポロジ構成はR2から見て隣接コストが全て「1」ですよね。あえてそうしました。コスト0はありえないので、これが最小でわかりやすいと思ったからです。
仮に、自分を経由した経路が隣接に伝わった場合(今回はR1に)、絶対に1以上は相手から見たFDに加算されているはずです。
なので、そのルートを隣接(今回はR1)が跳ね返してきたとしたら、R2は絶対に「もともと隣接(R1)に送ったルートに1以上加算した値をRDとして受け取る」はずです。
だから、現在のSuccessorのFDとFeasible Successor候補のRDを比較して、RDが大きければFeasible Successorになれないんです。「自分自身が投げたルートを返してきている可能性があるから」です。(他にも理由はあるかもしれませんが・・・)
今回の例では、左から来た(正確には跳ね返ってきた、ですがR2はそんな事知りません)ルートはRDが7であり、右のルートのFDより大きいのでFeasible Successorにはなれません。
まとめると、R2はこう考えます。
- R4からルートを貰ったとき
→初めて貰ったルートだからとりあえずSuccessor - R1からルートを貰ったとき
→僕が考えている目的地への最短距離と、R1が考えている目的地への最短距離を比較しよう。R1が考えている目的地への最短距離の方が遠い、ということはR1から貰ったルートは僕を経由したルートの可能性がある。だから排除。
INEのATCで言っているBrianの言葉を借りると「My cost of route to X is Y. Your cost of route to X is Z. If Z is higher than X, then I can’t guarantee your route is loop free path(私のXへのルートのコストはYです。貴方のXへのルートのコストはZです。もし、ZがXより大きい場合、私は貴方がくれたルートがループフリーだと保証できません)。
このロジックだと、自分自身がループさせてないか?しか分からない
トポロジ全体がループしていないかは、分かりません。
しかし、EIGRPに参加している全員が同じロジックを適用して、かつ「Successorしか広報しない」ルールを守っていたら、結果的にトポロジ全体がループフリーになるはずです。
だから、コストを算出するK値はEIGRPに参加している全員が同じでないとダメなんです。
再配送したらループを起こす可能性があるんです。
では、このロジックは万能か?
残念ながら、万能ではありません。
このロジックで検出できるのは、「自分自身が投げたルートを返してきている可能性がある」ルートです。
可能性があるルートです。
つまり、可能性があるルートは全て排除です。絶対って決めつけられないので、保守的にならざるを得ません。
以下の例を見てください。
これは、初めに出した例です。R1からみて、R1-R3の経路はFeasible Successorです。
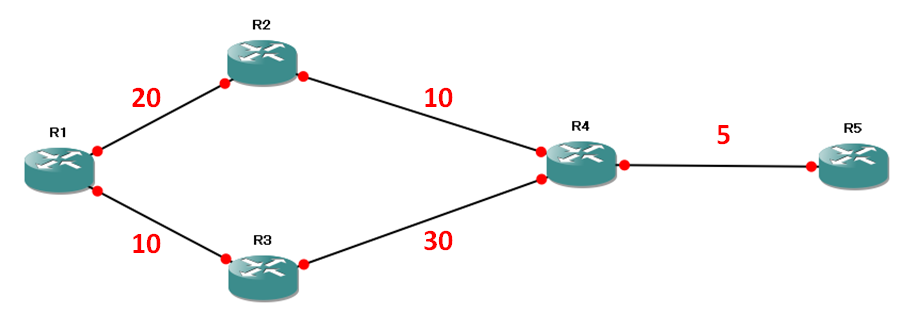
次に以下の例を見てください。
違いが分かりますか?R1-R3のコストとR3-R4のコストを逆転させました。
これだけで、R1からみてR1-R3の経路はFeasible Successorではなくなりました。
R1-R3の経路はループしていないのですが、R1からみてロジック的に可能性を捨てきれないので、除外しているのです。
これが、Distance Vectorの限界です。
いかがでしたか?
少しでもEIGRPのコンセプトの理解が固まったら幸いです。
以下、おまけです。CCIE勉強している方が対象です。
OSPFがリンクステートなのは同一エリア内だけであって、エリア間はDistance Vectorの性質を持つことを知っていると思います。
なので、上記と同じ問題が出てきます。いかに、エリア間でループフリーを保証するか?
OSPFはEIGRPとは別の方法で解を導き出しています。
OSPFは必ずエリア0が中心で、エリア0以外のエリアは絶対にエリア0を介さないと他のエリアに接続できません。
これによって、ループフリーを保っているのです。
EIGRPはOSPF等と違ってCisco Proprietaryなので、全ての仕様が公開されている訳ではありません。
「ここ間違ってるよ!」など、ご指摘がございましたら問い合わせフォームにてご連絡ください。




コメント